Inconnue et résultat |
Formalités
Le système- – l’alphabet :
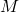 ,
, 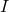 ,
, 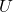 ;
; - – l’axiome :
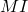 ;
; - – quatre règles :
- Ajouter un suffixe : si une chaîne se termine par
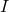 on peut ajouter un
on peut ajouter un 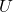 à la fin ;
à la fin ; - Répéter un élément : avec une chaîne
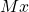 on peut former
on peut former 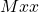 (quelque soit
(quelque soit 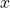 ) ;
) ; - Substituer : on peut remplacer
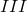 par
par 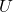 ;
; - Supprimer : on peut supprimer toute paire
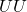 .
.
- Ajouter un suffixe : si une chaîne se termine par
|
|