Mathématiques et herméneutique

Autant un texte grec peut-il être interprété de multiples façons, autant le texte mathématique ne devrait avoir qu’une et une seule interprétation. Excepté dans des expressions comme ‘Soient a, b, c non nuls’ où seul le contexte permet de déterminer si des trois variables aucune n’est nulle ou si l’une d’elles peut être nulle pourvu qu’elles ne soient pas toutes trois simultanément nulles.

Qu’est-ce que ça dit ?
Différents niveaux d’interprétation ;
Repérer les passages obscurs ;
Y-a-t-il amphibologie ?
Passages parallèles : Raccorder, rassembler
Todorov : « Tellement pressé de tourner la page qu’on a même pas pris le temps de la lire »
Une parole qui s’attend à une réponse. (L’élève attend une note, une remarque…)
On lit, on écoute, on regarde avec nos préjugés. Le lecteur invente l’histoire. Est-ce possible en math ?
Les 3 vérités : physiques, sociales et psychique. Quid des maths ? [fvplayer id= »2″]
« Le signifiant n’a de sens que dans sa relation à un autre signifiant. » J. Lacan, « Du sujet enfin en question », Écrits, Seuil, 1966, p. 234.
Voire d’autres méthodes de recherche : archéologie, étude des monuments, …
Lire des mathématiques se réduit-il à lire du sens littéral ? N’y a-t-il pas de sens figuré ?
On trouve des glossaires, des dictionnaires (Baruk), la plupart des mots sont définis, le sont-ils tous ?
1. Doit-on considérer certains exercices (ou exemples) comme emblématiques, exemplaires,
  propres à faire comprendre quelque chose au delà de l’exercice proprement dit ? (allégorie ? )
  Sens caché ?
  ‘La lettre enseigne l’histoire, l’allégorie, ce à quoi tu crois ; le sens moral, ou tropologique, ce que tu fais ; l’anagogie, ce vers quoi tu tends’.
  Ce célèbre verset cité par Nicolas de Lyre au XIV° siècle, résume toute l’exégèse des pères de l’Eglise.
  p 439 (Sens littéral de « L’interprétation » ) La fusion, voire l’identification du sensus litteralis et du sensus historialis résulte du caractère narratif des Évangiles. Elle est propre à l’exégèse théologique des Écritures.
  Convient-il de lire uniquement d’un point de vue formel ou doit-il donner du sens à la lecture ? (cf Baruk, Si 7 = 0. Quelles mathématiques pour l’école ? ).
L’intelligence du texte n’est pas immédiate et requiert le commentaire de l’enseignant collectivement et parfois en tête à tête.
En admettant que les mathématiques soient une langue, sa traduction en français, en anglais ou tout autre langue se heurte à des obstacles d’une toute autre nature que la traduction « à la Google ». On est loin de la Novlang ! Et l’on peut interroger la fonction créatrice du langage (p 445) en math et ailleurs.
Équivalents des actes de parole (p 448) : interprétation du discours comme agir,
Polysémie du mot « signe » ! ! ! Signe du nombre, de la fonction, signe d’égalité (=) d’inégalité (<, >…) signe d’opération
Traduire les maths 3 exemples : https ://www.erudit.org/fr/revues/memoires/2017-v9-n1-memoires03394/1043118ar/
[…] Parallèlement, la partie réservée à l’algèbre dans le « Webber », tout comme dans les manuels domestiques, privilégie une présentation des savoirs et un ordre logique qui sont tous deux empruntés aux ouvrages de géométrie euclidienne. Ceux-ci ne recourent pas aux récents résultats de l’analyse et abondent en règles particulières et exemples applicatifs. Critique de cette méthode pour l’enseignement de l’algèbre, à l’instar de plusieurs autres pédagogues américains de l’époque[26], Farrar traduit les Éléments d’algèbre de Lacroix, ouvrage dans lequel l’auteur français propose une présentation des savoirs suivant l’ordre dans lequel l’esprit humain se les approprie graduellement, exposition jugée alors plus naturelle. En traduisant Lacroix, Farrar souhaite exposer « la métaphysique du calcul[27] », c’est-à-dire une science entière et cohérente, et non une suite segmentée de mécanismes opératoires. L’ouvrage préfère alors la généralisation des résultats à l’exposition d’une série de cas particuliers[28]. […]
Particularité plus intéressante, le traducteur mentionne également en avoir attendu un profit financier, ce qui ne se produit pourtant que rarement dans le cas des ouvrages de mathématiques. Cela peut expliquer le fait qu’il s’agisse d’une traduction littérale et non pas d’une adaptation, pratique courante dans l’espace germanophone et bien plus coûteuse en temps. L’auteur a tout de même converti les unités de mesure usuelles (monnaies, poids, longueurs, etc.) en leurs équivalents saxons et prussiens.[…]
Exemple de logique, p XI :
[…] Une analyse des intentions de discours (les buts illocutoires associés à l’expression). Un exemple : l’énoncé « Ne devrais-tu pas partir ? » n’est pas la preuve d’un comportement non-classique de la négation et d’une pluralité de significations de l’opérateur de négation : s’il équivaut à l’énoncé apparemment opposé « Tu devrais partir », c’est parce que la première expression est un acte interrogatif où le locuteur suggère l’accomplissement par l’interlocuteur de l’affirmation « Je vais partir ». Si les deux énoncés ci-dessus ne sont pas contradictoires, c’est parce qu’ils ne correspondent pas à deux énoncés déclaratifs opposés ; ils correspondent respectivement à une question (but illocutoire directif) et une promesse portant sur un même contenu propositionnel, c’est-à-dire deux actes directifs dont le but illocutoire est le même mais dont la force illocutoire n’est pas identique (suggérer le départ : « tu devrais partir », promettre le départ : « je vais partir »). Le logicien non-classique a selon nous le tort de ne pas tenir compte de cet aspect illocutoire du discours et de réformer la lettre des phrases avant de comprendre l’esprit de leur énoncé. […]

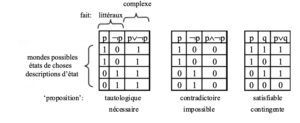
p 17 L’analogie entre les mondes possibles de la logique modale et les tables de vérité de la logique classique s’obtient en quantifiant sur des assignations de valeurs de vérité. Dans une table de vérité bivalente, chaque colonne indique une ‘proposition’ atomique reflétant un état de choses, et la dernière colonne indique une proposition exprimant un fait ; chaque ligne exprime un ensemble d’état de choses ou monde possible et détermine le statut ‘modal’ de la formule : la nécessité correspond à l’assignation de la vérité pour chaque ligne, l’impossibilité à l’assignation de la fausseté pour chaque ligne, la contingence à l’assignation de la vérité pour certaines lignes et de la fausseté pour d’autres.

p48 Comment garantir qu’un énoncé de langue allemande renvoie à la même croyance qu’un énoncé de langue française, par exemple ?
Mettre dans le contexte.
Pourquoi qualifier de « symbole » certains signes mathématiques ?
Le fil de la pensée dans l’exercice mathématique doit-il être considéré comme illusion par opposition avec la formalisme de l’écriture. Pourtant il arrive qu’un exercice soit résolu « de tête » avant de pouvoir être exprimé par écrit. Parfois même, il semble qu’un exercice soit résolu sans même y penser de façon « subconsciente ».
« Avoir faux » n’est pas le contraire de « avoir vrai » ! C’est plutôt, comme une phrase mal construite, qui ne respecte pas les règles.
On peut « avoir faux » et tomber « juste ».
Dans l’enseignement des mathématiques le mot « énoncé » n’a pas son sens habituel ? ?
Lire un « énoncé » c’est donner au texte une interprétation mathématique.
Connaître la définition de chaque mot « mathématique » et connaître suffisamment la définition des autres mots.
La définition d’un mot mathématique conduit la plupart du temps vers une solution. ( ex rectangle dans le 1/4 de cercle)
Nécessité du commentaire du texte mathématique.
Bouleau_Nicolas
L’outil principal est sémantique : inventer des idées simplifiantes. […]
Si l’on suit aujourd’hui la démarche de Descartes de s’inspirer de la rigueur mathématique pour ordonner sa pensée, force nous est de tenir compte de cette grande leçon des années trente : la fécondité et la puissance des mathématiques leur vient de méthodes abstraites et non de dénombrements exhaustifs.
[Sartre] met en effet le doigt sur le caractère théorique de la liberté cartésienne : une création scientifique qui nie la liberté de créer. Il fait à ce propos cette remarque simple mais philosophiquement essentielle : « Il entre toujours, dans l’ivresse de comprendre, la joie de nous sentir responsables des vérités que nous découvrons. Quel que soit le maître, il vient un moment où l’élève est tout seul en face du problème mathématique, s’il ne détermine pas son esprit à saisir les relations, s’il ne produit pas lui-même les conjectures et les schèmes qui s’appliquent tout comme une grille à la figure considérée et qui dévoileront les structures principales, s’il ne provoque enfin aucune illumination décisive, les mots restent signes morts, tout est appris par cœur ». Sartre a donc perçu l’importance et la fondamentale liberté du travail sémantique en mathématiques qui conditionne leur fécondité. […]
Ecrites aujourd’hui en un système de signes assez bien unifié, les mathématiques restent fondamentalement polysémiques et le travail du sens y est la dimension principale de créativité. […]
L’abstraction mathématique au contraire, qui elle est féconde, se présente comme un travail interprétatif où le sens qui vient à émerger parvient à éclairer des situations préalablement inextricables. Après la période moderne et la tentative unitaire de Bourbaki, le mathématicien redécouvre aujourd’hui une activité culturelle plus proche de celle des grands amateurs du passé.