Base

Titre : Bulletin de l’APMEP. N° 442. p. 650-657. A quel type de vérité les mathématiques peuvent-elles prétendre ?

Pour ce faire il [Hilbert] transforme l’arithmétique en un système formel.Deux remarques avant de poursuivre :

il formalise l’arithmétique, donc il y un contenu préexistant,
quand on est au niveau du système formel on n’est plus dans les ou la mathématique(s), mais dans la logique c’est-à-dire à un niveau métamathématique.

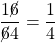
Le postulat finitiste de Hilbert a été mis en échec par Gödel.

L’acquis positif de cette limitation est l’apparition de la notion d’indécidabilité. […] on peut démontrer, en un nombre fini d’étapes que certains problèmes ne sont pas calculables, c’est à dire qu’il n’existe aucun algorithme pour les résoudre.

Au cours de la recherche ouverte par la question : « à quel type de vérité les mathématiques peuvent-elles prétendre ? » nous avons rencontré deux réponses négatives : les mathématiques ne relèveraient pas de la vérité matérielle de type empirique et, en tant que mathématiques, elles ne relèveraient pas de la vérité formelle de type calculabilité.

Les impasses relatives que constituent les solutions intermédiaires nous ont conduit à reformuler la question initiale et à chercher des pistes du côté des conditions historiques de la vérité mathématique.

Une certitude demeure : la question initiale renvoie au moins à un problème ouvert, peut-être à un problème indécidable. Les biais cognitifs et les fausses croyances

Biais de croyance

On peut simplifier une fraction par suppression d’un terme commun au numérateur et au dénominateur
$\dfrac{1\cancel{6}}{\cancel{6}4}= \dfrac{1}{4}$

Biais de confirmation

Biais de négativité

Biais de proximité

CC FR vérité mathématique philosophie 9+ Image d’avatar Vérité mathématique : vérité scientifique ?

13 minutes : Les planètes assimilées à des points / les photons non !

14 : traduction du réel en math

23 : signal et appareil de mesure (distance) . Fonctions Fourrier

24 :30 Extrait de pi (1999) Darren Aronofsky

32 : 98+3 = 101

« La science est l’asymptote de la vérité. Elle approche sans cesse, et ne touche jamais » (Victor Hugo). Jean-Pierre Kahane interroge les notions de vérité scientifique et de vérité mathématique. En physique, le critère de vérité d’une théorie est fondé sur la conformité aux faits. En mathématiques, c’est la relation entre le vrai et le démontrable qui fait preuve ; les mathématiques construisent leur vérité sur des axiomes et des théorèmes. La solidité des mathématiques tient aux démonstrations qui établissent la vérité des propositions à partir de celles qui sont déjà établies ou postulées. Comment se fait-il alors que les mathématiques soient si performantes pour décrire la réalité du monde physique ?

46 : Poincaré, vérité, faisceau de vérité, cohérence

49 : Vérité et pertinence

52 : Théorème et axiome, on s’arrête et … mathématique en mouvement

1 :08 : À une suite de nombres premiers, je peux tjrs en ajouter un nouveau

bijection entier/fraction … et pont de segment non !

1 :14 vérité non démontrable

Une démonstration est-elle éternelle ? Un théorème est-il éternel ?

La position du raisonnement mathématique par rapport à la vérité mathématique est analogue à celle des déductions du tribunal par rapport à la réalité extérieure. Un raisonnement juste est éternel mais il ne dévoile qu’une réalité partielle. Si l’on s’en tient même aux propriétés des entiers naturels, la plupart des propriétés vraies sont non démontrables à partir des axiomes de Peano. Un exemple simple est le fait que ce soit la tortue qui gagne dans la fable suivante du lièvre et de la tortue. L’on part d’un entier $n$ par exemple $n =9$ et on l’écrit en base $2$ . $9 = 2^3+1$ . On écrit aussi tous les exposants en base $2$ , et ainsi de suite s’il y a à nouveau des exposants, de sorte que dans notre exemple on écrit l’exposant $3 = 2 + 1$ et $9 = 2^{2+1}\; +1$ . Le lièvre arrive et remplace tous les $2$ par des $3$ , ce qui remplace $9$ par $3^{3 +1} + 1$ , la tortue soustrait $1$ . Le lièvre réécrit le résultat en base $3$ , puis remplace tous les $3$ par des $4$ , ce qui dans notre exemple donne $4^4 +1$ . La tortue soustrait $1$ . Le lièvre réécrit le résultat en base $4$ , ce qui donne $3\times 4^4 +3\times 4^3+3\times 4^2+3\times 4+3$ , puis remplace tous les $4$ par des $5$ , la tortue soustrait $1$ et ainsi de suite. Eh bien, l’on sait démontrer grâce à la théorie des nombres ordinaux que, comme dans la fable, c’est la tortue qui gagne, c’est-à-dire que quel que soit l’entier $n$ dont on parte, on arrivera toujours à $0$ au bout d’un nombre fini d’étapes, malgré les bonds prodigieux du lièvre ! L’on sait aussi que l’énoncé « pour tout $n$ c’est la tortue qui gagne » n’est pas démontrable au sein de l’arithmétique de Peano, d e même que la non-contradiction de cette arithmétique n’est pas démontrable en son sein ! On peut comprendre que le nombre de pas nécessaires est extrêmement grand en prenant l’exemple très simple $n = 4$ pour lequel le nombre de pas est de l’ordre de $10^{121210694}$ .

On prend un nombre naturel au hasard, par exemple $8$ et on l’écrit en base $2$ en utilisant que des puissances de 2.
$8 = 2^{2+1}$ Le lièvre arrive est remplace tout les $2$ par $3 \longrightarrow 3{3+1} = 81$ . On obtient un nombre bien plus grand car le lièvre court plus vite que la tortue.
La tortue arrive est soustrait $1 \longrightarrow 80$
Le lièvre écrit le nouveau nombre en base $3$ et remplace les $3$ par des $4 \longrightarrow 3^{3+1} - 1 = 3^3 \times 2 + 3^2 \times 2 + 3 \times 2 + 2 \longrightarrow 4^4 \times 2 + 4^2\times 2 + 4 \times 2 + 2$ La tortue elle soustrait toujours $1 \longrightarrow 4^4 \times 2 + 4^2 \times 2 + 4 \times 2 + 1 = 169$ Donc à chaque étape, on incrémente la base (le lièvre), et on soustrait 1 (la tortue).