Initial, ment ? |
- Ex 1 (Lebossé et Hémery, Quatrième p. 7) 11. Somme de plusieurs nombres algébriques. La somme de plusieurs nombres algébriques rangés dans un certain ordre est le nombre algébrique obtenu en ajoutant le premier nombre au second, le nombre obtenu au troisième, et ainsi de suite.
- Ex 2 (Ibid p. 10) 16. Définition. On appelle différence de deux nombres algébriques le nombre qu’il faut ajouter au second pour obtenir le premier.
- Ex 3 (Ibid p. 12) 21. Principes relatifs aux égalités.
1° Si deux nombres et
et 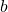 sont égaux, il en est de même des nombres
sont égaux, il en est de même des nombres 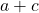 et
et 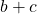 , ou des nombres
, ou des nombres  et
et 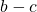 . Donc : On peut ajouter un même nombre aux deux membres d’une égalité.
. Donc : On peut ajouter un même nombre aux deux membres d’une égalité.
2° Si l’on a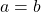
et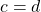
on a aussi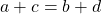
et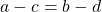
On peut ajouter ou retrancher des égalités membre à membre.
3° Considérons l’égalité (1)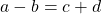 Ajoutons le nombre (b – d) aux deux membres ; nous obtenons :
Ajoutons le nombre (b – d) aux deux membres ; nous obtenons : 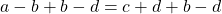 soit :
soit : 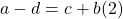
Le terme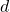 qui figurait dans le second membre de l’égalité (1) avec le signe + figure dans le premier membre de l’égalité (2) avec le signe – ; tandis que le terme
qui figurait dans le second membre de l’égalité (1) avec le signe + figure dans le premier membre de l’égalité (2) avec le signe – ; tandis que le terme 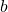 qui figurait dans le premier membre de l’égalité (1) avec le signe – figure dans le second membre de (2) avec le signe +. Donc : Dans une égalité on peut faire passer un terme d’un membre dans l’autre à condition de changer le signe qui le précède.
qui figurait dans le premier membre de l’égalité (1) avec le signe – figure dans le second membre de (2) avec le signe +. Donc : Dans une égalité on peut faire passer un terme d’un membre dans l’autre à condition de changer le signe qui le précède. - Ex 4 (Ibid p. 15) 25. Produit de plusieurs facteurs. Définition. On appelle produit de plusieurs nombres algébriques rangés dans un certain ordre le nombre algébrique obtenu en multipliant le premier facteur par le deuxième, le nombre obtenu par le troisième et ainsi de suite.
- Ex 5 (Ibid p. 23) 37. Somme de deux vecteurs portés par un même axe ou des axes parallèles. Considérons les deux vecteurs
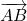 et
et 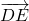 (figure 3) portés par les axes parallèles
(figure 3) portés par les axes parallèles 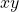 et
et 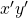 . Construisons par l’extrémité
. Construisons par l’extrémité 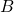 du premier un vecteur
du premier un vecteur 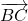 parallèle à
parallèle à 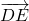 , de même sens et de même longueur :
, de même sens et de même longueur : 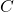 se place sur l’axe
se place sur l’axe 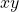 puisque les directions
puisque les directions 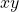 et
et 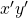 sont parallèles. Le vecteur
sont parallèles. Le vecteur 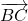 est dit égal au vecteur
est dit égal au vecteur 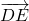 et le vecteur
et le vecteur 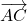 est par définition la somme des vecteurs
est par définition la somme des vecteurs 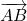 et
et 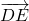 ou
ou 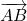 et
et 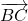 .
. *** QuickLaTeX cannot compile formula: \begin{tikzpicture}[scale=1] \draw[thick, -|] (0,1.5) node [below left] {$x'$} -- (4,1.5) node[above]{$E$} ; \draw[thick, red] (4,1.5) -- (6,1.5) ; \draw[thick, |-triangle 60] (6,1.5)node[above]{$D$}-- (9,1.5) node [below right] {$y'$} ; \draw[thick, -|] (0,0) node [below left] {$x$} -- (2,0) node[above]{$A$} ; \draw[thick, -|] (2,0) -- (4.75,0) node[above]{$C$} ; \draw[thick, red] (4.75,0) -- (6.75,0) ; \draw[thick, |-triangle 60] (6.75,0)node[above]{$B$}-- (9,0) node [below right] {$y$} ; \draw(4,-1) node {figure 3} ; \end{tikzpicture} *** Error message: Package tkz-fct Error: tkz-base must be loaded before tkz-euclide. leading text: \endinput}{} - Ex 6 (Ibid p. 37) 62. Degré d’un monôme. On appelle degré d’un monôme par rapport à une lettre l’exposant de cette lettre dans le monôme.
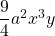 est du second degré en
est du second degré en  , du troisième en
, du troisième en 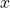 et du premier en
et du premier en 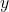 . Que faire ?
. Que faire ? - Ex 7 (Ibid p. 73) 509. Deux ouvriers gagnent ensemble 142,50 fr par jour. En un mois, le premier a travaillé 24 jours et le second 20 jours. Ils ont reçu ensemble 3116 fr. Quel est le salaire journalier de chacun ?
- Ex 8 (Ibid p. 74) 127. Nombres premiers. Un nombre premier est un nombre qui n’est divisible que par lui-même et l’unité. 13 est premier car ses seuls diviseurs sont 1 et 13. 25 n’est pas premier car il admet pour diviseurs 1, 5, 25.
- Ex 9 (Ibid p. 77) 522. Montrer que tout nombre premier supérieur à 5 est obligatoirement terminé par 1, 3, 7 ou 9. Décomposer en facteurs premiers les nombres suivants : 523. 108, 144, 2520, 8000
- Ex 10 (Ibid p. 78 et 79 ) 139. Nombres premiers entre eux. On appelle nombres premiers entre eux deux nombres qui n’admettent comme diviseur commun que 1. Autrement dit leur
PGCD est 1. Les nombres 36 = 22 × 32 et 25 = 52 sont premiers entre eux.
20101209_polysemie_et_langue_mathematique
Yves CittonLes données
Les données brutes sont un oxymores la « donnée brute » effacent toute trace des conditions de production … des conditions dans lesquelles les données sont ouvertes et diffusées ? … étudiées de près, s’apparente à un oxymore (Bowker, 2000; Gitelman, 2013).
Biens rival (ex. : crayon) et biens non rival (Le rêve de D’alembert)
datas et 0/1
discret / continu
résonances interférences, échantillonnage pertinences prélèvements hacker
hypertexte et recherche dans les traces
apprentissage et affect / plaisir
Où sont les maths ?
Visualisation du son, et inversement
Économie de l’attention, qu’est-ce que je vais regarder ?
Attention collective
Retard de l’attention, du temps pour y revenir
Comment anticiper mon attention ? Algorithme
Comment se construire humain+numérique

